Author: David Wu

The Seventh Day, Site Plans and EPC

Well, it’s been one full week of trying to get back into building my website. Although right now it’s just a collection of musings or ramblings on my usual go-to topics, I really do hope to expand out this website one day. Things like adding in-site Javascript code for games, posting more about philosophical topics, etc.

Anyways, tomorrow is the day of judgement for me, or for most other people, it’s just a regular old BMAB backgammon tournament. For my last minute preparations, I have researched my own version of a racing formula, used for short races, based on EPC. In fact, just as today is lucky day #7, EPC is based on 7s, the average roll of 2d6 without accounting for doubles, and in the formula I will be extending the definition of an N-roll position having an EPC of 7N+1 from rolls vs. rolls positions to pips vs. pips positions and pips vs. rolls positions. The formula, which assumes money game/neutral match score, roughly goes like this:

  • For the leader, who is the player on roll and considering doubling, find the closest N, such that 7N+1 is within ±3 pips of the leader’s actual EPC. Another way of saying this is that the leader has approximately an N-roll position. Remember that to derive the EPC from an “nice” pips position, simply add 7 (lucky day #7 strikes again)!
  • The borderline for offering an initial double occurs when the trailer has an EPC of N-5 more than the leader.
  • The borderline for offering a redouble occurs when the trailer has an EPC of N-4 more than the leader.
  • The take/pass borderline occurs when the trailer has an EPC of N-1 more than the leader. When the difference in EPC reaches N, the trailer had better pass!
  • The above formula works specifically for pips vs pips positions. In pips vs rolls (or rolls vs pips) positions, the leader has a bigger advantage, since the extra wastage generated by the rolls position means less variance for the trailer to make a comeback. Here, the double/no double borderlines should be moved back one pip, to N-6 and N-5, and the take/pass borderline should be moved back two pips, to N-3.

Of course, this formula is far from perfect, and will certainly undergo revisions in the future, but any rough formula is better than none when there is so much on the line tomorrow. A grandmaster title is at stake here, depending on whether I can play an average PR of 3.27 or better!

1234 Chess

For my software engineering senior design project, I had the pleasure of working with six of my classmates on an interface to play an abstract game I invented called “1234 Chess”. Although that was three years ago, 1234 Chess has not been forgotten. Instead, now it is back, in its new and improved form!

For those of you that are curious, here are the rules. The game is so simple, it only needs five rules to describe it in its entirety!

  1. 1234 Chess is an abstract board game, played by two players, White and Black, on a 10×10 board. Each player has 24 pieces: eleven 1-pieces, eight 2-pieces, three 3-pieces, and two 4-pieces. White moves first, then players alternate making moves until someone meets a victory condition, described at the very end.
  2. On your turn, you must move exactly one of your pieces. 1-pieces move exactly 1 square in any direction, like a chess king. 2-pieces move exactly 2 squares in any one direction, and can jump over an intervening piece. 3-pieces move exactly 3 squares in any one direction, and can jump over any intervening pieces. 4-pieces move exactly 4 squares in any one direction, and can jump over any intervening pieces. Jumped pieces belonging to either player are not affected whatsoever.
  3. You may not move one of your pieces to a square that is already occupied by one of your other pieces.
  4. If you move one of your pieces to a square that is occupied by one of your opponent’s pieces, of the two pieces, the lower numbered piece is captured and removed from the board. If both pieces are equally numbered, then both pieces are captured and removed from the board, in a so-called trade.
  5. There are two victory conditions in this game. Victory by Infiltration is when you advance one of your 1-pieces all the way to the farthest rank (the row where your opponent’s 3-pieces and 4-pieces started), and it is not captured by the start of your next turn. Victory by Elimination is when you capture all eleven of your opponent’s 1-pieces. The first player to meet either of these victory conditions wins the game. If both players’ last 1-pieces are simultaneously captured in a trade, the game is a draw. Also, if 100 moves go by without a capture being made, the game is a draw.

First Mahjong of 2025

Don’t get me wrong, I’m very glad to have won the first mahjong tournament of the new year. The only thing is, in the very first hand, I missed out on an opportunity for a monster hand, Three Identical Sequences (一色三同順).

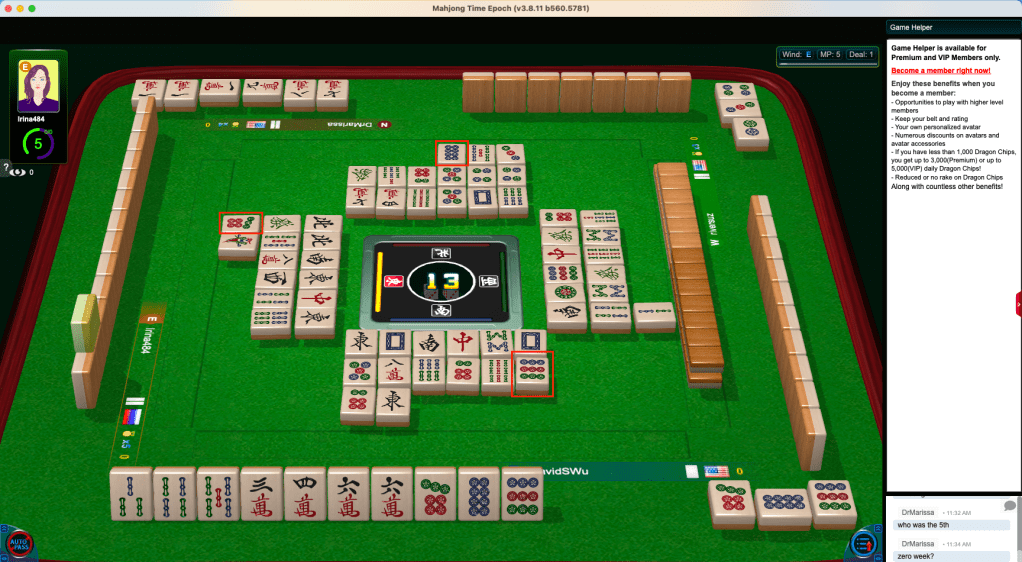
Waiting on 2/5 Characters, my next draw was the 5 Character and so I was able to go out and win 15 points from everyone with All Sequences (平和) + Two Identical Sequences (一般高).

However, look at the emphasized tiles in the discard! A few turns back, I drew a 9 Dot, which meant I had two choices: either discard the 9 Dot and keep waiting on my 15 point hand, or keep the 9 Dot, break the 34 Characters, and go for Three Identical Sequences. I decided against that, because A. it was already quite late in the game (24 tiles left in the wall at that time), B. it’s the first game of the match, so I’m not behind in the score or anything, and C. I’m already waiting for the win and with a completely live two-sided wait to boot! Alas, the very low probability event I didn’t want to see, happened before my very own eyes! Irina discarded the 7 Dot I could have Chowed, and Marissa discarded the 8 Dot I could have won on! I could have upgraded my 10 points from Two Identical Sequences, into 120 points from Three Identical Sequences! 125 points from everyone (well, strictly speaking, 315 points from Marissa and 30 points from the other two players) would have almost certainly sealed my victory for the match right from the very first game!

So I felt absolutely awful for the first half of that match, but as luck would have it, I would go on to win another big hand, which was good enough to win the match and tournament! As the hackneyed saying goes, all is well that ends well.

Backgammon Goals

With the NY Metro coming up next Wednesday, if I want to attain a Grandmaster title by the end of the BMAB tournament there, I will have to play at or better than a 3.27 PR. My checker play should be fine, but I must have a huge leak in my cube actions, especially when it comes to racing cubes and cubes at lopsided scores. Because of that, I will need to study some racing formulas, and also at the very least the doubling points/take points where the taker has no further use for the cube, apart from possibly an automatic redouble.

For example, I’ve heard Michy has memorized the gammonless take point at 3-away 2-away for the leader is 26%, but if I were to derive it myself so I can memorize it easier, it would be like this: Risk = 50% – 32.3% = 17.7%, Reward = 100% – 50% = 50%, Risk/(Risk+Reward) = 17.7%/67.7% = 26.1%. So basically spot on.

Nicomachus’s Theorem

Today I learned that the identity I noticed in my Foundations of Computer Science class, which was basically just a discrete math class, in freshman year of college 5 years ago has a name! It’s called Nicomachus’s Theorem, and it states that the sum of the first n cubes is equal to the square of the sum of the first n natural numbers*! For example, this year, 2025, can be expressed in both ways, using n = 9, as follows:

1³ + 2³ + 3³ + 4³ + 5³ + 6³ + 7³ + 8³ + 9³ = (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9)² = 2025

There is a beautiful proof without words from Wikipedia of this theorem:

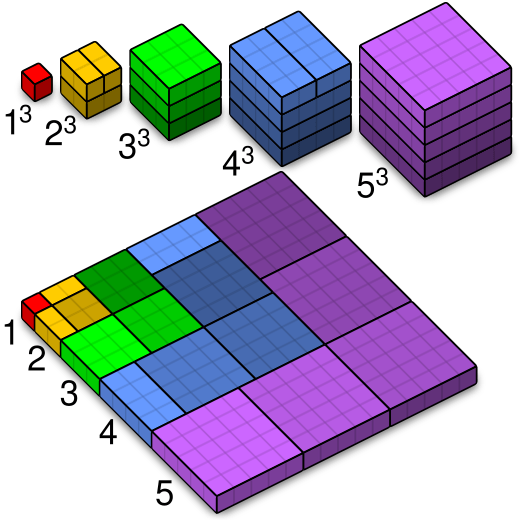
Unfortunately it stops at 5, but nonetheless, here’s to a lucky 2025!

*Yes, I am aware that 0 can be considered the first natural number. It does not change the correctness of this statement. If needed, it can be addressed by a substitution of n = m+1. So for example, as shown above by this year of 2025, since the statement is true for the first m = 9 natural numbers excluding 0, the statement is also true for the first n = 9+1 = 10 natural numbers including 0, since neither adding 0³ to the left hand side nor adding 0 to the right hand side inside the parentheses changes the value of any expression.