Today I learned that the identity I noticed in my Foundations of Computer Science class, which was basically just a discrete math class, in freshman year of college 5 years ago has a name! It’s called Nicomachus’s Theorem, and it states that the sum of the first n cubes is equal to the square of the sum of the first n natural numbers*! For example, this year, 2025, can be expressed in both ways, using n = 9, as follows:
1³ + 2³ + 3³ + 4³ + 5³ + 6³ + 7³ + 8³ + 9³ = (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9)² = 2025
There is a beautiful proof without words from Wikipedia of this theorem:
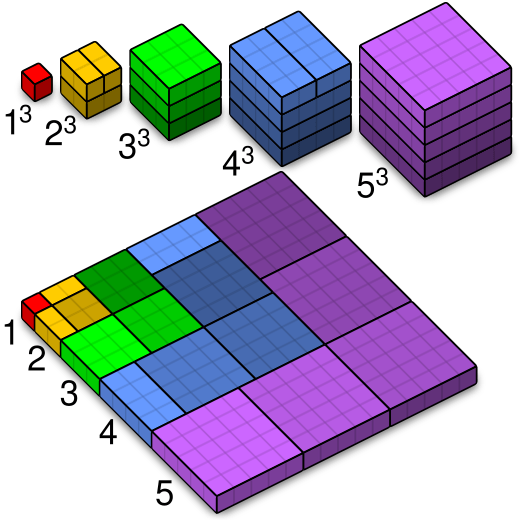
Unfortunately it stops at 5, but nonetheless, here’s to a lucky 2025!
*Yes, I am aware that 0 can be considered the first natural number. It does not change the correctness of this statement. If needed, it can be addressed by a substitution of n = m+1. So for example, as shown above by this year of 2025, since the statement is true for the first m = 9 natural numbers excluding 0, the statement is also true for the first n = 9+1 = 10 natural numbers including 0, since neither adding 0³ to the left hand side nor adding 0 to the right hand side inside the parentheses changes the value of any expression.